TD
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Page 1 : CY Cergy Paris Universite2024 – 2025CY TechPreIng 2Travaux diriges d’ElectromagnetismeCe document est disponible en ligne— 1/19 —
Page 2 : Table des matieres1. Distributions continues5I.Applications de cours . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5II.Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .62. Champ electrostatique7I.Loi de Coulomb . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7II.Calculs de flux de champ electrique . . . . . . . . . . . . . . . . . . . . . . . . . . . .8III.Calcul de champ electrique avec le theoreme de Gauss . . . . . . . . . . . . . . . . . .8IV.Lignes de champ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9V.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .93. Potentiel electrostatique10I.Gradient et champ electrique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10II.Calcul de potentiel et de champ electrique pour diverses symetries . . . . . . . . . . .104. Conducteurs a l’equilibre electrostatique11I.Proprietes des conducteurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11II.Calcul de la capacite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .125. Force de Lorentz13I.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .146. Champ magnetostatique15I.Loi de Biot et Savart . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .15II.Calcul de champ magnetique avec le theoreme d’Ampere . . . . . . . . . . . . . . . .15III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .167. Equations de Maxwell17I.Consequences des equations de Maxwell. . . . . . . . . . . . . . . . . . . . . . . . .17II.Applications des equations de Maxwell . . . . . . . . . . . . . . . . . . . . . . . . . .178. Induction19I.Phenomenes d’induction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19— 2/19 —
Page 3 : Plan du coursElectrostatiqueForce entre deux chargesChamp electriqueTheoreme de superposition et symetriesTheoreme de GaussPotentiel electrostatiqueConducteurs en equilibre electrostatiqueMagnetostatiqueChamp magnetique - Force de LorentzLoi de Biot et Savart - Theoreme de superposition et symetriesInduction electromagnetismeElectrodynamique des regimes quasi stationnairesIntensite et tensionEquations caracteristiques des principaux dipˆolesLois de KirchoffEquations de MaxwellEquations de MaxwellEquations de Maxwell dans le vide— 3/19 —
Page 4 : Contact— Enseignants charges du cours magistral : Emilie Dupont et Abdelaziz Boumiz— Bureau : Bˆatiment Cauchy Etage 3 CY 308— E-mail : emilie.dupont@cyu.fr— E-mail : abdelaziz.boumiz@cyu.frL’equipe pedagogiqueCours Magistral CM : Emilie Dupont Cergy, Abdelaziz Boumiz ; et Paul Fruton PauTravaux diriges TD :Panayotis Akridas Cergypanayotis.akridas-morel@cyu.frAbdelaziz Boumiz Cergyabdelaziz.boumiz@cyu.frLucie Desplat Paulucie.desplat@cyu.frEmilie Dupont Cergyemilie.dupont@cyu.frPaul Fruton Paupaul.fruton@cyu.frFabien Piguet Cergyfabien.piguet@cyu.frQuelques referencesListe non exhaustive de livres recommandes pour ce cours.— Jose-Philippe Perez, Robert Carles, Robert Fleckinger : « Electromagnetisme : Fondements etapplications », Dunod ; 4e edition 20 janvier 2020— « Le Cours de physique de Feynman »titre original : Feynman Lectures on Physics de RichardFeynman, Robert B. Leighton en et Matthew Sands en, Electromagnetisme 1.— Jerˆome Majou : « Super manuel de physique », MPSI, PCSI, PTSI, BrealConsultez le site du cours sur la plateforme.Allez voir aussi les sites : http://cpinettes.u-cergy.fr/S3-Electromag.html, https://etienneklein.fr/ ethttps://www.physagreg.fr/electromagnetisme1.php.Regarder la chaˆıne youtube sciences etonnantes... Il y a beaucoup de ressources en ligne, apprenez achoisir les bonnes et bien sˆur gare aux fakesciences— 4/19 —
Page 5 : 1Distributions continuesLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Applications de coursExercice 1 – Calculs d’aire et de volumeEn choisissant le systeme de coordonnees approprie :1/ Calculer, en utilisant une integrale double, la surface d’un disque de rayon R.2/ Calculer, en utilisant une integrale double, la surface de la paroi laterale d’un cylindre dehauteur h et de rayon R.3/ Calculer, en utilisant une integrale triple, le volume d’un cylindre de hauteur h et de rayon R.Exercice 2 – Calculs de charge totaleEn choisissant le systeme de coordonnees approprie :1/ Calculer la charge totale contenue dans un fil de longueur L uniformement charge dont ladensite lineique vaut λ0.2/ Calculer la charge totale contenue dans un disque de rayon R uniformement charge en surfacedont la densite surfacique vaut σ0.3/ Calculer la charge totale contenue dans une boule de rayon R uniformement chargee en volumedont la densite volumique vaut ρ0.ExercicesExercice 3 – Charge totale d’une distribution surfaciqueOn considere une sphere de centre O et de rayon R portant en sa surface une densite de chargesσ = σ01 + cos θou θ = →Oz, →OP.Calculer la charge totale portee par la distribution.Exercice 4 – Noyaux atomiques Du point de vue du potentiel et du champ electrique qu’ils creent, les noyaux de certains atomes legerspeuvent ˆetre modelises par une distribution volumique de charge a l’interieur d’une sphere de centreO et de rayon a. On designe par →r = →OP, le vecteur position d’un point P quelconque de l’espace.Pour r a, la charge volumique ρP qui represente le noyau varie en fonction de r suivant la loi :ρr = ρ0 1 r2a2!ou ρ0 est une constante positive.— 5/19 —
Page 6 : 1/ Donner les symetries et invariances de cette distribution de charges.2/ Exprimer la charge totale Q du noyau.Pour aller plus loinExercice 5 – Masse volumique de la TerreOn peut supposer, dans un modele grossier, que la repartition de la masse de la Terre assimilee a unesphere de rayon R n’est pas uniforme : le noyau terrestre, principalement forme de fer et de nickel,est plus dense que la croˆute. La masse volumique ρ depend donc de la distance r au centre C :ρr = ρ01 r2RDonnees : la densite du fer vaut environ 8 et celle des roches granitiques vaut environ 4.1/ Exprimer la masse M de la Terre en fonction de R et ρ0.2/ Calculer numeriquement la masse volumique au centre et a la surface de la Terre. Commenter.On donne M = 6.0 × 1024 kg et R = 6.4 × 103 km— 6/19 —
Page 7 : 2Champ electrostatiqueLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Loi de CoulombExercice 1 – Distribution discrete de charges ponctuellesQuatre charges electriques ponctuelles, de valeur absolue q, sont placees aux sommets d’un carreABCD. Ce carre a pour cˆote 2a, centre O et appartient au plan Oxz, comme le montre la figureci-dessous.Determiner l’expression de la force subie par la charge electrique Q placee en un point M quelconquede l’axe Oy.— 7/19 —
Page 8 : Calculs de flux de champ electriqueExercice 2 – Symetrie spheriqueSoit une sphere, de rayon R, chargee uniformement.En commen¸cant par une etude de symetrie et d’invariance, calculerle flux de →E a travers la surface Σ d’une sphere de rayon r. Lesdeux spheres ont le mˆeme centre.Exercice 3 – Symetrie cylindriqueSoit un cylindre, de rayon R et de hauteur supposee infinie, chargeuniformement.En commen¸cant par une etude de symetrie et d’invariance, calculerle flux de →E a travers la surface Σ d’un cylindre de rayon r et dehauteur h. Les deux cylindres ont le mˆeme axe.Exercice 4 – Symetrie planeSoit un plan infini charge uniformement de densite σ.En commen¸cant par une etude de symetrie et d’invariance, calculerle flux de →E a travers la surface Σ d’un cylindre de rayon r et dehauteur h. L’axe du cylindre est perpendiculaire au plan charge.il serait interessant de prendre h/2 de part et d’autre du plan.Calcul de champ electrique avec le theoreme de GaussExercice 5 – Sphere uniformement chargee en volumeUne boule de centre O et de rayon R porte une densite volumique de charge uniforme ρ.1/ Quelle est l’expression de la charge totale, notee Q, contenue dans la sphere ?2/ Calculer le champ electrostatique →E M en considerant le point M :a a l’interieur de la sphere : r Rb a l’exterieur de la sphere : r R3/ Le champ est-il continu a la traversee de la sphere ? A commenter.4/ Tracer l’allure de Er.Exercice 6 – Sphere uniformement chargee en surfaceUne sphere de centre O et de rayon R porte une densite surfacique de charge uniforme σ.1/ Quelle est l’expression de la charge totale, notee Q, sur la sphere ?2/ Calculer le champ electrostatique →E M en considerant le point M :a a l’interieur de la sphere : r Rb a l’exterieur de la sphere : r R3/ Le champ est-il continu a la traversee de la sphere ? A commenter.4/ Tracer l’allure de Er.— 8/19 —
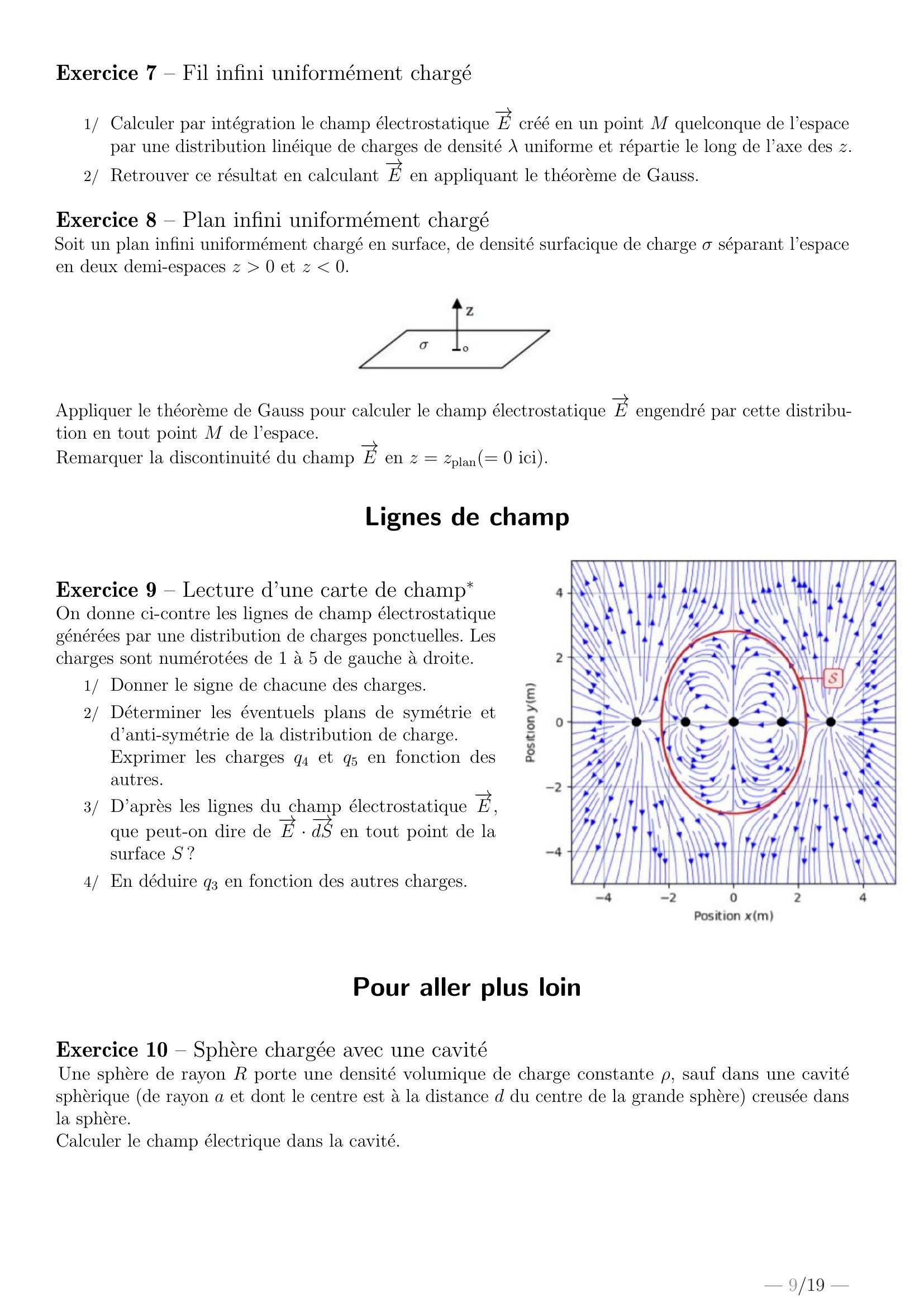
Page 9 : Exercice 7 – Fil infini uniformement charge1/ Calculer par integration le champ electrostatique →E cree en un point M quelconque de l’espacepar une distribution lineique de charges de densite λ uniforme et repartie le long de l’axe des z.2/ Retrouver ce resultat en calculant →E en appliquant le theoreme de Gauss.Exercice 8 – Plan infini uniformement chargeSoit un plan infini uniformement charge en surface, de densite surfacique de charge σ separant l’espaceen deux demi-espaces z 0 et z 0.Appliquer le theoreme de Gauss pour calculer le champ electrostatique →E engendre par cette distribu-tion en tout point M de l’espace.Remarquer la discontinuite du champ →E en z = zplan= 0 ici.Lignes de champExercice 9 – Lecture d’une carte de champOn donne ci-contre les lignes de champ electrostatiquegenerees par une distribution de charges ponctuelles. Lescharges sont numerotees de 1 a 5 de gauche a droite.1/ Donner le signe de chacune des charges.2/ Determiner les eventuels plans de symetrie etd’anti-symetrie de la distribution de charge.Exprimer les charges q4 et q5 en fonction desautres.3/ D’apres les lignes du champ electrostatique →E ,que peut-on dire de →E · →dS en tout point de lasurface S ?4/ En deduire q3 en fonction des autres charges.Pour aller plus loinExercice 10 – Sphere chargee avec une caviteUne sphere de rayon R porte une densite volumique de charge constante ρ, sauf dans une cavitespherique de rayon a et dont le centre est a la distance d du centre de la grande sphere creusee dansla sphere.Calculer le champ electrique dans la cavite.— 9/19 —
Page 10 : 3Potentiel electrostatiqueLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Gradient et champ electriqueExercice 1 –Determiner les coordonnees de →gradf ou f est le champ scalaire suivant :1/ fx, y, z = xy2 yz22/ fx, y, z = xyz × sinxy3/ On donne le champ scalaire fx, y, z = x2 + y2 + z2. Calculer →gradf.Discuter les symetries et invariances des champs f et →gradf.Exercice 2 – Calcul de potentiel electriqueLe potentiel cree par une charge ponctuelle en un point M, situe a la distance r de la charge q, est aune constante additive pres :V M =14πε0qrCalculer le champ electrostatique →E qui derive du potentiel V .Calcul de potentiel et de champ electrique pour diversessymetriesExercice 3 – Symetrie spheriqueSoit une sphere de centre O et de rayon R cf. exercice 6 du TD2. Determiner le potentiel electrostatiquecree par la distribution surfacique de charges de densite σ repartie uniformement sur la surface decette sphere.Exercice 4 – Symetrie cylindriqueSoit un cylindre de rayon R et de hauteur infinie. Determiner le potentiel electrostatique cree par ladistribution surfacique de charges de densite σ repartie uniformement sur la surface de ce cylindre.Exercice 5 – Symetrie axiale Un champ de vecteur →E derive d’un potentiel V qui a la symetrie de revolution autour de l’axe Oz.On se place dans un plan contenant l’axe Oz. Dans ce plan, on adopte les coordonnees polaires, etl’on pose θ = →Oz, →OM. Le potentiel V a alors pour expression :V =Kr3 3 cos2 θ 1Determiner les composantes du champ →E .— 10/19 —
Page 11 : 4Conducteurs a l’equilibre electrostatiqueLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Proprietes des conducteursExercice 1 – Conducteur creuxSoit A, un conducteur creux.On place en son sein un second conducteur note B portant une charge +Q :1/ Retrouver le fait que QA,int = QB = Q en utilisant le theoreme de Gauss. On note QA,int :charge surfacique presente au niveau de la surface interieure de A.2/ Calculer la charge exterieure QA,ext i.e. charge surfacique presente au niveau de la surfaceexterieure de A dans les cas suivants :a A est isole et initialement neutre.b A porte une charge initiale qCalcul de la capaciteExercice 2 – Condensateur planUn condensateur plan, place dans le vide ε0, est constitue de deux armatures conductrices planes desurface S, paralleles entre elles, et separees d’une distance e l’une de l’autre.Dans cette etude, on se place dans l’approximation d’un condensateur plan infini.— 11/19 —
Page 12 : 1/ En utilisant le theoreme de Gauss, determiner le champ electrostatique →E cree par un planinfini charge avec une densite de charge surfacique uniforme +σ.2/ Deduire le champ entre les deux armatures du condensateur en fonction de la charge surfacique+σ puis en fonction de la charge totale +Q portee par l’armature n◦1.3/ En deduire la difference de potentiel V = V1 V2 entre les armatures n◦1 et n◦2, puis lacapacite C du condensateur en fonction de S, e et ε0.4/ Application numerique :Pendant un orage, la surface de la Terre et la surface inferieure des nuages forment, avec uneassez bonne approximation, un condensateur plan. On suppose que le nuage se trouve a 1000metres d’altitude et qu’il couvre une surface d’environ 20 km2.Quelle est la valeur de la capacite du condensateur forme par le systeme « Terre Nuage » ?Donnees : ε0 = 8.85 × 1012 SIExercice 3 – Condensateur cylindriqueUn condensateur cylindrique a air est forme de deux armatures coaxiales, de rayons notes R1 et R2avec R1 R2. Ces deux cylindres infinis coaxiaux sont uniformement charges en surface avec unecharge Q1 et Q2 respectivement, telles que Q1 = Q2 = Q.1/ On suppose ici que ce conducteur est de longueur infinie. Determiner →E en un point M situe ala distance r de l’axe, avec R1 r R2.2/ En deduire l’expression de la capacite C de ce condensateur. A.N. : R2 = 20 cm, R1 = 10 cmet h = 50 cm.3/ Que devient l’expression de la capacite C lorsque les rayons sont voisins c-a-d : R2 R1 = e R1.Pour aller plus loinExercice 4 – On considere deux boules conductrices de rayons R1 et R2 dont les centres sont a une distance dgrande devant R1 et R2. Elles portent les charges respectives Q1 et Q2, distribuees uniformement.1/ Calculer les potentiels V1 et V2 de chacune des boules, en leur centre.2/ On relie les boules par un fil conducteur. Calculer les charges Q1′ et Q2′, ainsi que les potentielsnotes V1′ et V2′.3/ En deduire la capacite de ce conducteur constitue des deux boules reliees par le fil conducteur.— 12/19 —
Page 13 : 5Force de LorentzLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Exercice 1 – Force magnetique sur une charge en mouvement1/ Un proton se deplace vers la droite a 3000 m/s dans un champ de 10 G oriente dans la directionindiquee sur la figure.Quelle est la force sur ce proton ? Donner l’expression litterale de cette force puis sa valeurnumerique.2/ Une charge de 1 µC se deplace dans une region ou le champ magnetique est uniforme etconstant.Elle ne subit pas de force quand elle se dirige avec une vitesse de 5 m/s dans la direction del’axe des x positifs. Elle subit cependant une force de 107 N dans la direction de l’axe des zpositifs quand elle a une vitesse de →v = 3→i + 4→j m · s1.Les vecteurs unitaires de la base cartesienne sont : →i vecteur unitaire de l’axe x, →j vecteurunitaire de l’axe y et →k vecteur unitaire de l’axe z.Quel est le champ magnetique ?Exercice 2 – Force de LorentzUn proton q = 1,60 × 1019 C, m = 1,67 × 1027 kg se trouve dans un champ magnetique uniformed’intensite B = 0,5 T. On appelle x l’axe qui pointe dans la direction de ce champ.A t = 0 s, le proton a une vitesse →v avec vxt = 0 = 1,5 × 105 m · s1, vyt = 0 = 0 m · s1 etvzt = 0 = 2,0 × 105 m · s1.De plus, on est au point 0, 0, 0.1/ A l’aide de la deuxieme loi de Newton, ecrire les equations differentielles du premier ordre pourvx, vy et vz a t ⩾0 s.On notera →Ω= qm→B ,2/ Etablir les deux equations differentielles du second ordre pour vy et vz.3/ Montrer que la trajectoire du proton est une helice qui a pour axe la droite parallele a xd’equation z = 0; y = R, pour rayon R = vzt = 0Ωet de pas vxt = 02πΩ.— 13/19 —
Page 14 : Exercice 3 – Spectrometre de masseOn envoie un atome de krypton ionise 1 fois avec une vitesse de 40 000 m · s1 dans un spectrometrede masse ou regne un champ magnetique uniforme et constant de 0,6 T. L’atome frappe la plaque aune distance de 11,044 cm du point d’entree de l’atome.1/ Quelle est la masse de l’atome ?2/ De quel isotope de l’atome pourrait-il s’agir ?Pour aller plus loinExercice 4 – Particule dans des champs electrique et magnetiqueUne particule de masse m et de charge q penetre avec une vitesse →v 0 = v0→u x dans une zone ou existentun champ electrique →E = E0→u y et un champ magnetique →B = B0→u z uniformes et stationnaire.1. A quelle condition le vecteur vitesse de la particule reste-t-il inchange ?2. Expliquer comment ce dispositif peut ˆetre adapte en selecteur de vitesse.Exercice 5 – Particule dans des champs electrique et magnetiqueOn considere un point materiel de charge q 0 et de masse m, de vitesse initiale →v 0 a l’entreed’une zone ou regnent un champ electrique →E ou un champ magnetique →B . On suppose ces champsuniformes et independants du temps, et on neglige toute autre force que celles provoquees par ceschamps.La particule decrit une droite et possede une acceleration constante a.1. Determiner la direction et la norme du ou des champs qui provoquent cette trajectoire.2. Determiner la position du point materiel en fonction du temps.La particule decrit une trajectoire circulaire de rayon R0 dans un plan xOy.1. Determiner la direction du ou des champs qui provoquent cette trajectoire.2. Determiner la norme du champ en fonction de v0 et R0.— 14/19 —
Page 15 : 6Champ magnetostatiqueLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Loi de Biot et SavartExercice 1 – Fil rectiligne infiniment long1/ Calculer, par integration en utilisant la loi de Biot et Savart, le champ magnetique →B cree enun point M quelconque par un fil rectiligne infiniment long et defini par l’axe Oz.2/ Retrouver ce champ magnetique →B en appliquant le theoreme d’Ampere.Exercice 2 – SpireCalculer, par integration en utilisant la loi de Biot et Savart, le champ magnetique →B direction, senset module cree en un point M de l’axe de revolution d’une spire de centre O et de rayon R parcouruepar un courant d’intensite I constante.Calcul de champ magnetique avec le theoreme d’AmpereExercice 3 – Soleno¨ıde fini On considere un soleno¨ıde fini de longueur L et comprenant N spires, chacune etant parcourue parun courant d’intensite I constante.Ces spires sont circulaires de rayon R et sont regulierement enroulees sur un cylindre de revolutionautour de l’axe z′z.On cherche a determiner completement le champ magnetique →B M en un point M quelconque del’axe z′z.Le courant et l’axe z′z sont orientes de maniere directe regle du tire-bouchon.1/ Soit une longueur elementaire dz de l’axe z′z ou se trouve le soleno¨ıde. Quel nombre elementairedN de spires se trouvent entre la cote z et z + dz ?2/ Calculer le champ elementaire d→B M cree au point Mpar ces dN spires ?3/ En deduire la valeur Bz du champ magnetique au point Mz. On fera apparaˆıtre les anglesα1 et α2 sous lesquels on voit, du point M, la spire d’entree et la spire de sortie du soleno¨ıde.4/ Retrouver l’expression du champ magnetique →B M a l’interieur d’un soleno¨ıde infinimentlong, en utilisant le resultat precedent.5/ Retrouver l’expression du champ magnetique →B M a l’interieur et a l’exterieur d’un soleno¨ıdeinfiniment long en utilisant le theoreme d’Ampere.— 15/19 —
Page 16 : Pour aller plus loinExercice 4 – Tore circulaireOn veut etudier le champ magnetique cree par une distribution de courants presente sur un torecirculaire de rayon R a section circulaire de rayon a. On note O le centre du tore et Oz son axe derevolution. Une chambre a air gonflee, de velo par exemple, constitue un tel tore.La distribution de courants est constituee par un enroulement d’un grand nombre de N spires jointivescirculaires de rayon a enroulees sur toute la surface du tore, le sens du courant etant donne sur lafigure. On negligera l’epaisseur des fils.Soit M un point quelconque de l’espace ou l’on cherche le champ magnetique →B cree par cettedistribution.1/ Etude qualitativea Quel est le domaine de definition du champ magnetique ? Dans toute la suite, on considereque M appartient a ce domaine.b Quelle est la direction de →B en M ? Justifier la reponse.c Que vaut →B au point O ?d Justifier le choix du systeme de coordonnees cylindriques d’axe O, z. De quelles coor-donnees depend le module →B du champ ?2/ Montrer qu’en tout point situe a l’exterieur du tore, →B est nul.3/ Determiner l’expression de →B en un point quelconque de l’interieur du tore.— 16/19 —
Page 17 : 7Equations de MaxwellLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Consequences des equations de MaxwellExercice 1 – Equations de PoissonEtablir les equations de Poisson vues en cours.V + ρε0= 0→→A + µ0→j = →0Exercice 2 – Cylindre parcouru par un courantEn utilisant les equations locales de Maxwell, determiner le champ magnetique cree par un cylindreplein, infiniment long, de rayon R, parcouru par un courant uniforme I, suivant sa longueur.Exercice 3 – Champ electriqueDans le demi-espace vide x 0, il regne un champ electrique →E →r , t = E0cosωt kz.→e x, encoordonnees cartesiennes, avec ω et k deux constantes positives.1. Calculer div→E . Justifier le resultat obtenu.2. Calculer →rot→E et donner l’expression de l’equation de Mawxell faisant intervenir la quantite→rot→E .3. Determiner ainsi le champ magnetique →B →r , t. On supposera que →B n’a pas de terme constant.4. Verifier la valeur de sa divergence.5. Determiner la relation entre les constantes ω et k, a l’aide d’une autre equation de Maxwell,exprimee dans le vide.Applications des equations de MaxwellExercice 4 – Equation de Maxwell-GaussUne sphere creuse, de rayon interne R/2 et de rayon externe R, est chargee, avec une charge de densitevolumique de charge ρr. La charge totale portee par cette sphere est egale a Q.Le champ electrostatique cree a la distance r du centre O, pour R/2 r R a pour expression→E = kαr R→u r ou →u r est le vecteur unitaire radial de la base de coordonnes spheriques. Le milieuest assimilable au vide.1. Exprimer →E 0.— 17/19 —
Page 18 : 2. Etablir l’expression de →E r pour 0 r R/2 a partir des equations locales de Maxwell. Endeduire la valeur de α.3. Etablir la loi ρr. Calculer la charge totale et deduire la valeur de k.4. A l’exterieur de la sphere, les resultats obtenus sont-ils compatibles avec le theoreme de Gauss ?Exercice 5 – Cylindre conducteurSoit un cylindre conducteur de conductivite σ, de longueurh consideree comme infinie, parcouru par un courant sta-tionnaire uniformement reparti, dans la direction de son axe,d’intensite I.1. Determiner le champ electromagnetique en tout point de l’espace.2. En deduire le vecteur de Poynting en tout point de l’espace et son flux a travers la surfacecylindrique du conducteur. Commenter le resultat obtenu.3. Verifier l’equation locale de Poynting en tout point. Commenter.— 18/19 —
Page 19 : 8InductionLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Phenomenes d’inductionExercice 1 – Roue de BarlowUn disque conducteur de rayon a est libre de tourner autour de son axe horizontal passant par O. Uncourant constant d’intensite i arrive en son centre O et repart par le point A, sur la peripherie. Laroue est placee dans un champ magnetique horizontal, d’intensite B, uniforme et permanent.Calculer le moment Σ en O de la force de Laplace exercee sur le disque conducteur.Exercice 2 – Rail de LaplaceLa barre AB, de longueur a et de masse m, de centre de masse d’abscisse xt et de vitesse →v = v→uxavec v = ˙x est lancee avec une vitesse initiale v0 sur des rails metalliques sur lesquels elle glisse sansfrottement.Elle constitue avec les rails de resistance negligeable un circuit rectangulaire C de resistance Rconstante et d’inductance negligeable et dont la surface a l’instant t est St = axt.Ce circuit est place dans un champ magnetique permanent →B = B→uz d’origine exterieure a C.1/ Determiner la fem induite.2/ En deduire l’expression du courant induit qui circule dans la barre.3/ Etablir l’equation differentielle de vt et en deduire l’expression de la solution en tenant comptedes conditions initiales.4/ Montrer que l’energie cinetique initiale de la barre se dissipera totalement en chaleur par effetJoule dans la resistance.— 19/19 —